「A Beautiful Supertask」는 뉴턴 역학의 비결정적 측면을 지적하는 역설에 관한 논문입니다. 지난 시간 제논의 역설들을 다루면서 우리는 제논의 전제 중 “무한히 많은 과제를 하기 위해서는 무한히 많은 시간이 든다.”가 거짓이라는 것을 받아들였습니다. 한정된 시간 안에 연속적으로 일어나는 무한한(그러나 셀수 있는) 수의 과제를 초작업supertask이라고 합니다. 논문에서 제시된 초작업을 이해하기 위해 먼저 뉴턴 역학의 주요한 속성을 짚고 넘어가겠습니다.
먼저 뉴턴 역학은 시간 역전에 대칭적time-reversal symmetry입니다. 시간을 역전시킨 운동을 가정했을 때, 그 운동 역시 뉴턴 법칙을 따르는 것입니다. 자연 현상들 중엔 이런 시간 역전 대칭성을 가진 것들이 있고 그렇지 않은 것들이 있는데, 뉴턴 역학이 다루는 현상들은 모두 시간 역전에 대칭적인 것으로 알려져 있습니다. 이를 간단한 수식으로 나타내면 다음과 같을 것입니다.
\[m \frac{d^2}{dt^2}x(t) = F(x)\] \[x_r(t):=x(-t)\] \[m \frac{d^2}{dt^2}x_r(t) = F(x_r)\]또한 뉴턴 역학은 결정적deterministic입니다. 어떤 상태건 시간적으로 그 이전 상태에 의해 결정되는 것입니다. 이를 인과율을 따른다고 표현하기도 합니다. 뉴턴 역학의 체계 안에서 움직이는 것에는 움직이게 하는 것이 있다고 알려져 있습니다. 참고로 이러한 결정성은 현대의 양자 역학에서는 받아들여지지 않는 가정입니다.
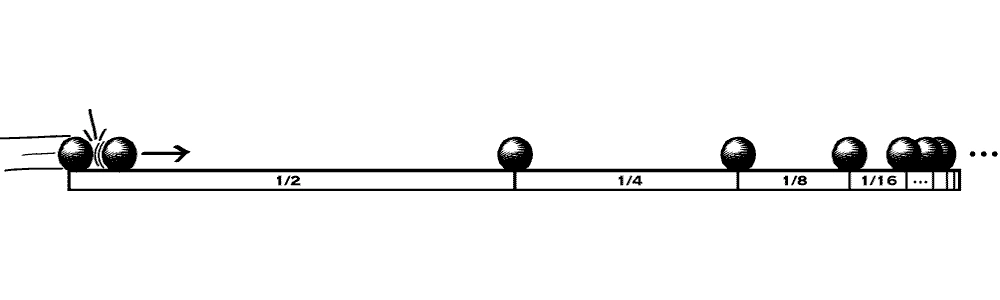
Jon Perez Laraudogoitia의 아름다운 초작업에 대해 간단히 정리합니다. 각각을 $ P_i $ ($i \in \{ 0, 1, 2, \ldots \} $)로 이름지을 수 있는 무한히 많고 질량이 같은 입자들이 좌표 $ X_{i}=1/2^i $ 에 위치해 있습니다. $ P_0 $ 가 $ P_i $ 을 향해 속력 $ \nu $ 로 움직이는 것 외에 다른 모든 입자는 정지해있고 이 때의 시각은 0입니다.

입자들의 충돌은 완전 탄성 충돌이며 질량이 동일하므로 충돌시 서로의 속력을 교환하게 됩니다. 따라서 $ P_0 $ 가 $ P_1 $ 에 충돌하면 $ P_0 $ 는 $ X_1 $ 에 정지하고, $ P_1 $ 은 $ P_2 $ 를 향해 속력 $ \nu $ 로 움직일 것입니다.
$ P_0 $ 와 $ P_1 $ 가 충돌하기까지 걸리는 시간은 \(\frac{X_0 - X_1}{\nu} = \frac{1}{2 \nu}\)
입니다.
그 후 $ P_1 $ 이 $ P_2 $ 에 충돌하기까지는 \(\frac{X_1 - X_2}{\nu} = \frac{1}{2^2 \nu}\)
시간이 걸립니다.
정리하면 각각의 연쇄적인 충돌들이 일어나는데까지 걸리는 시간은 다음과 같습니다.
\[\frac{1}{2 \nu}, \frac{1}{2^2 \nu}, \frac{1}{2^3 \nu}, \ldots\]따라서 모든 충돌이 일어나기까지 걸리는 시간은 이 수열의 합인 $ 1/\nu $가 되고 이후 계는 다음과 같은 상태가 됩니다.
- $ P_i $ 는 $ X_{i+1} $ 에 정지한다.
- 어떤 $ P_i $ 도 $ x=0 $ 에 도달하지 않는다.
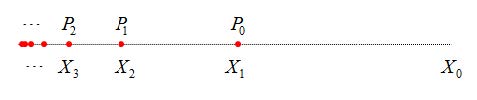
무한한 횟수의 충돌이 $ 1/\nu $라는 한정된 시간에 일어났으므로 이는 초작업입니다. 여기서 나타나는 첫 번째 문제는 역학적 에너지가 보존되지 않는 점입니다. 처음 $ P_0 $ 에 있던 운동 에너지가 나중에는 온데간데 없이 사라집니다. 이는 저자가 논문에서 중요하게 생각하는 문제는 아닙니다만, 제시된 초작업이 뉴턴 역학의 해라는 점에서 역설적입니다.
Jon Perez Laraudogoitia가 주목하는 초작업은 다음입니다. 언급된 모든 과정들을 비디오 카메라로 찍은 후, 필름을 역순으로 재생했다고 합시다. 물리학에서는 이런 방법을 두고 시간 역전을 시킨다고 말합니다. 그리고 앞선 예시는 뉴턴 역학으로 설명되어야 할 과정이므로, 시간 역전을 시킨다 해도 뉴턴 역학에 의해 설명되어야 합니다.
비디오를 역재생시키면 정지해있던 모든 $ P_i $ 가 $ X_{i+1} $ 에서 원래 자신이 차지하고 있던 $ X_i $ 로 돌아갑니다. 마침내 역재생된 비디오 안의 계는 $ 1/\nu $ 시간 후에 다음 그림과 같은 상태가 될 것입니다.
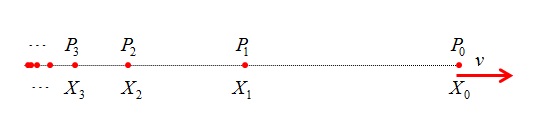
이 결과에서는 모든 $ P_i $ 의 위치가 최초와 같고, $ P_i $ 의 속도가 반대 방향이라는 점에서 시간 역전이 잘 되었다는 점이 확인됩니다. 그런데 여기서 초작업을 유발한 입자가 무엇인지에 관해, 결국 뉴턴 역학의 결정성에 대한 역설이 발생합니다. 즉, 역재생된 비디오를 보건대 정지해있던 입자들은 최초인이 없는 것으로도 보이는데도 운동을 시작하고 제자리로 돌아갑니다. 정지해있는 모든 입자들은 뉴턴 역학에 의하면 정지해야 하는데, 이 계는 자발적으로 운동을 시작하는 것입니다.
역설은 전제의 거짓됨이나, 논증의 부당함, 혹은 실제로는 그것이 건전하다는 것을 보임으로써 풀립니다. 그런데 이 역설을 발생하게 하는 지점이 어디인가에 답하는 것은 아주 어려워 보입니다. 이 역설은 특수 상대론적으로도 발생하는 것이라서, 최대 속도의 유한함이나 강체의 실재 여부에 대한 고려로는 풀리지 않습니다. 인과율은 뉴턴 역학에서는 아주 자명하다는 것을 겪어온 우리라서 결정성을 부정하는 것은 직관적이지 않습니다. 뉴턴 역학에서 시간 역전 대칭성이 지켜지지 않는 상황들이 있어 본 역설이 그에 속한다 하더라도 에너지 보존 법칙 위배는 여전히 문제입니다.
한가지 주목할만한 점은 이러한 일이 물리적 현실에서 일어날 수 있는가입니다. 이 논평에서 제시된 역설은 크기가 없는 점 입자를 가정했는데, Jon Perez Laraudogoitia는 논문에서 입자 $ P_i $ 를 반지름이 $ R_i = 1/2^{i+1} $인 구로 수정하여도 역설이 유효하다는 점을 지적했습니다. 크기가 아주 작은 입자, 그리고 그들 간의 거리가 굉장히 작은 스케일이라면 양자 역학적인 설명을 필요로 합니다. 그런데 입자의 위치와 운동량까지 특정되는 것은 양자 역학의 불확정성에 위배됩니다. 또한 입자의 인덱스가 클수록 밀도가 무한히 커진다는 문제가 발생합니다. 입자가 무한히 많은(셀 수 있는 무한과 대응되는) 상황이 물리적으로 실재할 수 있는지도 의문입니다. 특수 상대성에서 보건대 이 계는 전체 정지 질량 에너지가 무한이기 때문입니다. 이러한 상황은 우리가 다뤄온 좋은 사례들과는 다릅니다.